第２回若手奨励賞（領域11）
受賞者の発表
本年7月会告に従って、第2回若手奨励賞（領域11）の募集を行い、本年8月23日 に締め切りました。申し合わせに従って設置された領域１１の審査委員会による厳 選な審査の結果、応募の中から下記の4名の候補者が選考され、11月の理事会で 受賞者として承認されました。ここで、その受賞を祝福するとともに、領域１１関係 者に公示致します。 なお、授賞式ならびに受賞講演が2008年3月の年次大会にて行われますので、 会員の皆さんの講演会へのご参加をよろしくお願い致します。
| 受賞者 | 受賞題目 |
|---|---|
| 間田 潤（東京大学） | 周期箱玉系の研究 |
| 御手洗菜美子（九州大学） | 粉体斜面流の運動論的解析によるレオロジー特性の解明 |
| 笹本智弘（千葉大学） | 非平衡定常系の模型の厳密解 |
審査経過報告
領域１１における審査は、前回と同様、領域代表が指名した９名の審査委員により、メールを用いて行われた。審査委員は、領域１１が対象とする非常に幅広い分野をカバーするべく選ばれた方々である。うち１名が審査委員長を務め（審査委員長についても領域代表が指名）、選出の取りまとめに当たった。なお今回は、審査委員9名のうち3名が前回審査時から新メンバーへと交代した。前回と同様の手順により審査を進め、最終的には9名の審査委員全員によるメール投票を行って、今回は領域11から3名の授賞候補者を決定した。なお今回は、前回からあまり間を置かずに2回目を行ったという事情もあって、応募者数が前回に比べ大幅に減少した。次回以降、関連の皆様の積極的な応募を期待したい。
受賞理由
- 間田 潤氏 ： 周期箱玉系の研究
間田氏の研究は周期箱玉系に関するものである．箱玉系は，ソリトン的なふるまいをするセルオートマトン系を，箱の中を移動する玉のなす離散力学系として表現したものである．箱玉系は超離散化と呼ばれる手法によって KdV 方程式と結びつくことが示される一方で，可解格子模型との関連も明らかになり発展が注目されている．周期箱玉系はこの箱玉系に周期境界条件を課したものである．状態数が有限な可逆力学系であるため，すべての軌道は有限な長さの周期軌道になる．この軌道の長さ（基本周期）を具体的に評価することは非常に興味深い．というのは，この基本周期は可積分系とエルゴード性を持つ力学系とを区別するひとつの指標と考えられるからである．
間田氏は玉の密度を一定にしたまま箱の数（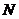
）を無限大にした際の基本周期の漸近挙動を調べ，基本周期の最大値は exp[
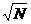] のオーダーであるが，ほとんどすべての基本周期は exp[(log 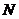)2 ] より小さいことをつきとめ，結果的にエルゴード性を持たないことを示した．さらに，整数論の重要な未解決問題であるリーマン予想が正しいことと周期箱玉系の基本周期の漸近形がある形をとることとが同値であるという数学的にも興味深い事実を指摘した．
周期箱玉系は，ある一般化6頂点模型の絶対零度の極限で得られる．間田氏はこの可解格子模型の絶対零度の極限での転送行列が周期箱玉系の時間発展を記述し，周期箱玉系の基本周期がこの転送行列の固有値から得られることを示した．さらに，転送行列の固有値，固有ベクトルを計算するときに使われるベーテ仮設方程式の変形パラメーターq が 0付近のときの解に関するストリング仮説と周期箱玉系の保存量との間の重要な関係を得た．この関係は量子可積分系と周期箱玉系の対応関係を明らかにするだけでなく，ストリング仮説の意味を明らかにする上でも重要なものである．
また，周期箱玉系の初期値問題は，周期離散戸田方程式の逆散乱法を媒介とする方法や量子群の表現論を用いる方法で解かれていたが，間田氏は初等的な方法で周期箱玉系の初期値問題を直接解くことに成功した．
以上の業績は一連の共同研究の成果であるが，間田氏はすべてにおいて中心的役割を果たしている．これらの業績は最近の箱玉系理論の進展に大きく寄与するもので若手奨励賞に値するものと認められる．箱玉系は日本で生まれ，日本で発展した．今後もこのようなユニークな研究が我が国から発信されることを期待したい． -
御手洗菜美子氏 ： 粉体斜面流の運動論的解析によるレオロジー特性の解明
粉体流の微視的な理論として、分子気体運動論を非 弾性衝突に拡張した粉体運動論がある。しかし、重力下における粉体斜面流に対しては、約50年前にBagnoldによって次元解析から得られた応力のスケーリング関係式が知られていたものの，運動論からの理解は遅れていた。御手洗氏はまずBagnoldスケーリングが運動論から導出できることを示し、その帰結として粉体の体積占有率が斜面の角度のみで決まること、さらには垂直応力やせん断応力も粒子の平均2乗速度（粉体温度）で規格化すると体積占有率で決まることを予測し、シミュレーションと良い一致を得ることに成功した。しかし、一方で実験では粉体の占有率は斜面の角度の減少関数であるのに対して、運動論は逆の予測を与え、またエネルギー散逸も高密度領域で大きくずれることを指摘した。
この問題を解決するため御手洗氏は中西氏との共同論文で、粉体のMDシミュレーションと運動論の詳細な比較を行い、高密度領域に関して運動論はエネルギー散逸と垂直応力を過大に評価していることをつきとめた。また、その原因は衝突の垂直相対速度の減少にあると予想し、衝突温度という量を定義することにより、実際に高密度領域で衝突速度が分子カオスから予想される値に比べ小さくなっていることを明確に示すことに成功した。そして、高密度領域での運動論からのずれは粒子運動に相関が生じるためであることを明らかにした。
粉体流のレオロジーを一般的に記述する為の、統一的な理論は未だない。御手洗氏の研究は運動論からスケーリング関係式を導き，さらに速度相関の重要性を明らかにするものであり、粉体流のレオロジーの理論発展に重要な寄与をおこない，若手奨励賞を受賞するにふさわしい． -
笹本智弘氏 ： 非平衡定常系の模型の厳密解
笹本智弘氏は，ある種の非平衡統計力学の模型の厳密解を求め，非平衡定常状態における相転移の様相を解明した。
笹本氏の研究で最も重要なものは，非対称排他過程(ASEP)と呼ばれる模型の定常状態を, q変形された直交多項式を用いて厳密に記述した業績である。ASEPは，1次元格子上に古典的な粒子が配置され，排除体積効果を持ちながら左右にドリフトする過程を記述する模型である。左右への遷移確率が対称の場合は問題が厳密に解けることが従来から知られていたが，非対称の場合は極めて複雑になり，q変形された量子群と関連した数理的にも興味深い問題になる。この一次元開放系において，笹本氏は大学院在学中に独力で，従来の研究が到達していた制約を大きく超える条件下（任意の非対称レート，任意の流入率，流失率）で厳密解を導出し，非平衡相転移の様相を幅広く明確に記述することに成功した。
笹本氏はこの研究以後も，(1) 結晶成長過程における界面のゆらぎに関するランダム行列理論を用いた厳密な解析や，(2) ある2成分非対称排他過程において，シミュレーションや平均場近似から相転移と思われていた現象が，実は数学的な特異性を伴わないクロスオーバーであり，しかもクロスオーバーであるという事実は，数値計算では到達不可能な極めて大きなサイズで初めて見えてくるということを厳密解で示すなど，非平衡統計力学の数理解析において注目すべき業績を上げ続けている。
以上の理由により，笹本智弘氏は第2回物理学会若手奨励賞受賞にふさわしいものと判断される。
授賞式
第63回年次大会において領域11の若手奨励賞授賞式が行われました。第二回目 の今回は間田潤氏（東京大学）、御手洗菜美子氏（九州大学）、笹本智弘氏 （千葉大学）の3名が受賞され、その受賞講演もあわせて行われました。
第二回若手奨励賞（領域11）受賞者の皆さん。左から間田潤氏、御手洗菜美子氏、笹本智弘氏。
受賞の言葉
受賞者の皆様から、受賞の言葉をいただきました。なお、所属は受賞時のものです。
間田潤氏（東京大学大学院数理科学研究科）
これまで地道に行ってきた研究に対し、若手奨励賞というすばらしい賞を授与していただき、どうもありがとうございました。これまでの苦労が報われたという思いと、研究にお力添え下さった先生方や周りの方々への感謝の気持ちで一杯です。 私が研究テーマとする‘箱玉系’は、箱と玉だけからなるものすごく簡単な対象であるにもかかわらず、非線形方程式の解がもつ性質を示したり、懸賞金が掛けられるような難解な問題（リーマン予想）と関わりをもったりと大変興味深い対象です。私の拙い講演では、その奥深さを十分に伝えられなかったと思っていますが、講演をお聞きいただいた方々に箱玉系、さらには超離散系について知っていただき、多少なりとも興味をもっていただけたのであれば嬉しい限りです。 若手奨励賞は始まったばかりであり、今後、どのような意味をもち、役割を果たすのか、受賞者の活躍によるところが大きいと考えます。大きなプレッシャーではありますが、受賞者の一人としての自覚をもち、これからも研究に勤しんでいきたいと思います。
御手洗菜美子氏（九州大学）
このたびは、若手奨励賞をいただき、ありがとうございます。多くの方々にいただいたご指導、ご意見、励ましが研究の原動力となっています。この場を借りて御礼申し上げます。また、賞のおかげで、広い分野の方々に研究を知っていただく機会をいただき、大変うれしく思います。時には流体のように、時には固体のように振る舞う、粉体というどこかつかみどころのない相手についての研究を評価していただきましたが、せっかくいただいた機会はしっかりつかんで、今後に生かせるように、励みたいと思います。
笹本智弘氏（千葉大学）
私が主として研究しているのは、体積排除効果をもつ１次元の多粒子拡散過程です。一見非常に単純なモデル系なのですが、物理的にも数学的にも豊富な内容を持っており、しかもまさに現在その性質がどんどん明らかにされつつあるという状況にあります。私自身その魅力にとり付かれ、かれこれ１０年以上研究してきました。その中でいくつかの発見もあったのですが、今回それらの成果を若手奨励賞という形で認めて頂き、大変嬉しく思います。これは、これまで研究上およびそれ以外でお世話になった先生、友人等、数多くの方々のお陰です。この場を借りて皆様に深く感謝致します。今後はより広く高い視点に立ち、これまでの研究をさらに発展させて行きたいと考えています。
日本物理学会 領域11